PålitelighetsteoriBadekarskurven
Den velkjente badekarskurven er hyppig brukt som illustrasjon på et typisk sviktmønster. Og for folk i vedlikeholdsbransjen er det er lett å kjenne igjen mønsteret: Først avtar antall svikt etter å ha vært høyt rett etter installasjonsfasen, for så å bli etterfulgt av en lang, stabil fase. Til slutt går kurven oppover igjen og avspeiler et økende antall problemer typisk forbundet med økende alder på utstyret. Når de 3 ulike sviktmønstre settes sammen, fås en badekarskurve som i Figur 1.

Badekarskurven benyttes ofte som en fin illustrasjon på hvorfor tidsbaserte utskiftninger eller overhalinger ikke er velegnet i kampen for å forbedre driftssikkerheten. For når mesteparten av kurven er konstant eller fallende, er det heller ikke noe poeng med periodiske utskiftninger eller overhalinger i samme tidsrommet. Slik presenteres kurven ofte, men så enkelt er det ikke.
Forutsetninger for badekarskurven er ikke oppfylt
For det første er utgangspunktet i badekarskurven at den er sammensatt av en enkelt hasardrate som både er minkende, økende og konstant. Men forutsetningene for dette er sjelden oppfylt. For å få en hasardrate må dataene tilhøre samme levetidsfordeling og være fra ikke-reparerbare enheter. Derfor er det lite troverdig når mange påstår at dette er en typisk hasardrate for installert utstyr. Det kan ikke utelukkes at de har produsert en badekarskurve med dataene sine, men det er lite trolig en hasardrate.
Alt forfaller
Problemet blir også tydelig i det som er den vanlige tolkningen av den horisontale delen. Delen gir en konstant hasardrate, men det er lite intuitivt i forhold til fysikkens lover som sier at alt forfaller med tiden (termodynamikkens 2. lov om økende entropi). I stedet for en konstant hasardrate, burde det ses en gradvis degradering. Årsaken er brudd på to nødvendige forutsetninger (ikke reparerbare enheter og identisk fordelte data), og kurven vil feilaktig vise et stykke med konstant hasardrate.
Misforståelsen oppstår når badekarskurven representerer utstyr eller systemer som vedlikeholdes. Vanligvis tenker man i vedlikeholdssammenheng på reparerbare enheter (for eksempel en pumpe) som består av ulike utskiftbare eller reparerbare deler. Fordi summen av alle hasardrater automatisk gir en horisontal kurve, er det uunngåelig at utstyret får en periode som viser en tilsynelatende, konstant hasardrate (Figur 2) fordi pumpen repareres. NB! Den horisontale linjen for systemer eller reparerbare enheter er den totale ROCOF (Rate of OCcurances Of Failures) og er noe helt annet enn hasardraten.

Badekarskurven villeder
Når feil fordeler seg jevnt utover tiden som i den horisontale del av badekarskurven, kan utstyret likevel bestå 100 % av komponenter med kraftig, økende hasardrate og likevel vil dataanalysen feilaktig vise en tilsynelatende konstant hasardrate . Og deler som har en økende tendens til svikt, vil også kunne ha et økonomisk, best mulig tidspunkt for periodisk utskiftning – altså stikk motsatt av hva den flate kurven gir inntrykk av.
En annen, negativ effekt ved tolkning av feil som “tilfeldige” (eng. random) er en distansering fra årsaken. For tilfeldige feil vil lett kunne oppfattes som enkelthendelser, og da blir også rasjonalatet for rotårsaksanalyse og forebygging borte. Men alt har en årsak – også feil som tilsynelatende framstår som tilfeldige. Mange av disse er også gjengangere som det er viktig å ta tak i.
Den virkelige badekarskurve
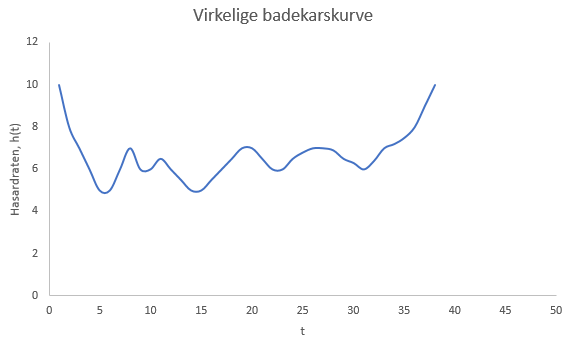
Kurven framstilles vanligvis som i Figur 1, men denne er en stilisert og eksisterer nok mest i undervisningsmateriell. Også ROCOF`en i Figur 2 er stilisert, og i virkeligheten vil det beste budet på en reell badekarskurve mest se ut som nedenfor i Figur 3 og ansporer ikke til bastante konklusjoner om bestemte vedlikeholdstaktikker.
Badekarskurven med liten praktisk betydning
Heldigvis er denne slags kurver ikke viktige for et godt vedlikeholdsprogram. Det er uansett forebygging av svikt som bør være fokus og ikke når ting svikter. For langt de fleste tilfeller er tiden bedre brukt på en runde med vibrasjonsmåleapparatet og forbedringstiltak enn forsøk på optimering av vedlikeholdet med statistiske beregninger med tvilsomme data.
Menu
PålitelighetsteoriBadekarskurven
Den velkjente badekarskurven er hyppig brukt som illustrasjon på et typisk sviktmønster. Og for folk i vedlikeholdsbransjen er det er lett å kjenne igjen mønsteret: Først avtar antall svikt etter å ha vært høyt rett etter installasjonsfasen, for så å bli etterfulgt av en lang, stabil fase. Til slutt går kurven oppover igjen og avspeiler et økende antall problemer typisk forbundet med økende alder på utstyret. Når de 3 ulike sviktmønstre settes sammen, fås en badekarskurve som i Figur 1.

Badekarskurven benyttes ofte som en fin illustrasjon på hvorfor tidsbaserte utskiftninger eller overhalinger ikke er velegnet i kampen for å forbedre driftssikkerheten. For når mesteparten av kurven er konstant eller fallende, er det heller ikke noe poeng med periodiske utskiftninger eller overhalinger i samme tidsrommet. Slik presenteres kurven ofte, men så enkelt er det ikke.
Forutsetninger for badekarskurven er ikke oppfylt
For det første er utgangspunktet i badekarskurven at den er sammensatt av en enkelt hasardrate som både er minkende, økende og konstant. Men forutsetningene for dette er sjelden oppfylt. For å få en hasardrate må dataene tilhøre samme levetidsfordeling og være fra ikke-reparerbare enheter. Derfor er det lite troverdig når mange påstår at dette er en typisk hasardrate for installert utstyr. Det kan ikke utelukkes at de har produsert en badekarskurve med dataene sine, men det er lite trolig en hasardrate.
Alt forfaller
Problemet blir også tydelig i det som er den vanlige tolkningen av den horisontale delen. Delen gir en konstant hasardrate, men det er lite intuitivt i forhold til fysikkens lover som sier at alt forfaller med tiden (termodynamikkens 2. lov om økende entropi). I stedet for en konstant hasardrate, burde det ses en gradvis degradering. Årsaken er brudd på to nødvendige forutsetninger (ikke reparerbare enheter og identisk fordelte data), og kurven vil feilaktig vise et stykke med konstant hasardrate.
Misforståelsen oppstår når badekarskurven representerer utstyr eller systemer som vedlikeholdes. Vanligvis tenker man i vedlikeholdssammenheng på reparerbare enheter (for eksempel en pumpe) som består av ulike utskiftbare eller reparerbare deler. Fordi summen av alle hasardrater automatisk gir en horisontal kurve, er det uunngåelig at utstyret får en periode som viser en tilsynelatende, konstant hasardrate (Figur 2) fordi pumpen repareres. NB! Den horisontale linjen for systemer eller reparerbare enheter er den totale ROCOF (Rate of OCcurances Of Failures) og er noe helt annet enn hasardraten.

Badekarskurven villeder
Når feil fordeler seg jevnt utover tiden som i den horisontale del av badekarskurven, kan utstyret likevel bestå 100 % av komponenter med kraftig, økende hasardrate og likevel vil dataanalysen feilaktig vise en tilsynelatende konstant hasardrate . Og deler som har en økende tendens til svikt, vil også kunne ha et økonomisk, best mulig tidspunkt for periodisk utskiftning – altså stikk motsatt av hva den flate kurven gir inntrykk av.
En annen, negativ effekt ved tolkning av feil som “tilfeldige” (eng. random) er en distansering fra årsaken. For tilfeldige feil vil lett kunne oppfattes som enkelthendelser, og da blir også rasjonalatet for rotårsaksanalyse og forebygging borte. Men alt har en årsak – også feil som tilsynelatende framstår som tilfeldige. Mange av disse er også gjengangere som det er viktig å ta tak i.
Den virkelige badekarskurve
Kurven framstilles vanligvis som i Figur 1, men denne er en stilisert og eksisterer nok mest i undervisningsmateriell. Også ROCOF`en i Figur 2 er stilisert, og i virkeligheten vil det beste budet på en reell badekarskurve mest se ut som nedenfor i Figur 3 og ansporer ikke til bastante konklusjoner om bestemte vedlikeholdstaktikker.
Badekarskurven med liten praktisk betydning
Heldigvis er denne slags kurver ikke viktige for et godt vedlikeholdsprogram. Det er uansett forebygging av svikt som bør være fokus og ikke når ting svikter. For langt de fleste tilfeller er tiden bedre brukt på en runde med vibrasjonsmåleapparatet og forbedringstiltak enn forsøk på optimering av vedlikeholdet med statistiske beregninger med tvilsomme data.