PålitelighetsteoriMTTF
MTTF er gjennomsnittlig levetid og benyttes kun for enkeltkomponenter – aldri for systemer eller reparerbare komponenter. For gjennomsnittlig tid før feil for reparerbare komponenter eller systemer, benyttes i stedet MTBF. Det betyr at alle levetider som registreres for identifisering av hazardrate (hazardrate er kun for ikke-reparerbare komponenter) er første svikt. Svikt nummer to på samme komponenten eksisterer ikke. For etter første svikt kasseres komponenten og erstattes av en ny. Om den nye komponenten er overhalt eller «fabrikkny» er selvfølgelig uvesentlig – eneste krav er at den skal oppføre seg på samme måte som en ny og at klokken «nullstilles».
Data må tilhøre samme levetidsfordeling
Komponenter må også ha samme driftsbetingelser slik at dataene tilhører samme levetidsfordeling, altså at levetidene genereres av samme underliggende prosess. Det krever at installasjon må være korrekt, vedlikeholdet må være det samme og driftsbetingelsene må være de samme. For eksempel kan samme type ventil gi levetider fra ulike, underliggende prosesser dersom ventilene sammenstilles på ulik måte eller medium har ulik temperatur. Flere, underliggende prosesser tilsvarer å ha flere levetidsfordelinger og blir å blande epler og pærer og det er ikke mulig å lage en meningsfull modell, som for eksempel en weibullfordeling.
Dersom alle levetidene kommer fra samme prosess og derfor kun har en levetidsfordeling kan denne plottes som i Figur 1. Kommer levetidene fra ulike prosesser finns det ikke en f(t), R(t), F(t) eller MTTF.
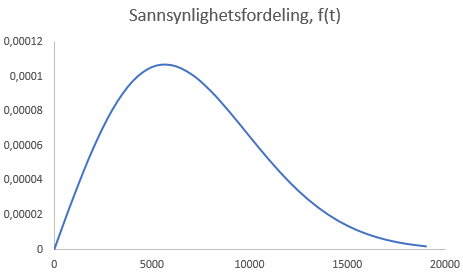
Når kravene er oppfylt for å kunne modellere en f(t), er ![]()
To typer data
En meningsfull MTTF krever at dataene er fra samme sannsynlighetsfordeling, og vi sier at levetidene er identisk fordelte. Dessverre er tilgjengelig data er stort sett alltid observasjonsdata som er en slags biprodukt av produksjonen. Dataene stammer vanligvis ikke fra eksperimenter hvor forutsetningen alltid er at dataene er identisk fordelte.
I et produksjonsmiljø med observasjonsdata er denne forutsetningen et veldig strengt krav som ikke kan tas for gitt. For driftsbetingelser er hele tiden i endring og faren blir stor for å blande ulike levetidsfordelinger. Spørsmålet blir da om driftsforholdene er tilstrekkelig identiske til å kunne beregne en meningsfull MTTF. Virkeligheten i et produksjonsmiljø taler dessverre for at betingelsene ofte ikke er oppfylt. Men for at matematikken ikke skal bryte sammen, er det helt nødvendig at levetidene er forutsigbare. Med forutsigbarhet menes ikke at levetider kan forutses nøyaktig, men at prediksjoner er mulige med sannsynlighetsteori. Dette bryter sammen dersom ikke levetidene er identisk fordelte.
For å lage en korrekt hasardrate, h(t), kreves det at levetidene oppfyller kravene til å være grunnlag for MTTF beregning.
Menu
PålitelighetsteoriMTTF
MTTF er gjennomsnittlig levetid og benyttes kun for enkeltkomponenter – aldri for systemer eller reparerbare komponenter. For gjennomsnittlig tid før feil for reparerbare komponenter eller systemer, benyttes i stedet MTBF. Det betyr at alle levetider som registreres for identifisering av hazardrate (hazardrate er kun for ikke-reparerbare komponenter) er første svikt. Svikt nummer to på samme komponenten eksisterer ikke. For etter første svikt kasseres komponenten og erstattes av en ny. Om den nye komponenten er overhalt eller «fabrikkny» er selvfølgelig uvesentlig – eneste krav er at den skal oppføre seg på samme måte som en ny og at klokken «nullstilles».
Data må tilhøre samme levetidsfordeling
Komponenter må også ha samme driftsbetingelser slik at dataene tilhører samme levetidsfordeling, altså at levetidene genereres av samme underliggende prosess. Det krever at installasjon må være korrekt, vedlikeholdet må være det samme og driftsbetingelsene må være de samme. For eksempel kan samme type ventil gi levetider fra ulike, underliggende prosesser dersom ventilene sammenstilles på ulik måte eller medium har ulik temperatur. Flere, underliggende prosesser tilsvarer å ha flere levetidsfordelinger og blir å blande epler og pærer og det er ikke mulig å lage en meningsfull modell, som for eksempel en weibullfordeling.
Dersom alle levetidene kommer fra samme prosess og derfor kun har en levetidsfordeling kan denne plottes som i Figur 1. Kommer levetidene fra ulike prosesser finns det ikke en f(t), R(t), F(t) eller MTTF.

Når kravene er oppfylt for å kunne modellere en f(t), er ![]()
To typer data
En meningsfull MTTF krever at dataene er fra samme sannsynlighetsfordeling, og vi sier at levetidene er identisk fordelte. Dessverre er tilgjengelig data er stort sett alltid observasjonsdata som er en slags biprodukt av produksjonen. Dataene stammer vanligvis ikke fra eksperimenter hvor forutsetningen alltid er at dataene er identisk fordelte.
I et produksjonsmiljø med observasjonsdata er denne forutsetningen et veldig strengt krav som ikke kan tas for gitt. For driftsbetingelser er hele tiden i endring og faren blir stor for å blande ulike levetidsfordelinger. Spørsmålet blir da om driftsforholdene er tilstrekkelig identiske til å kunne beregne en meningsfull MTTF. Virkeligheten i et produksjonsmiljø taler dessverre for at betingelsene ofte ikke er oppfylt. Men for at matematikken ikke skal bryte sammen, er det helt nødvendig at levetidene er forutsigbare. Med forutsigbarhet menes ikke at levetider kan forutses nøyaktig, men at prediksjoner er mulige med sannsynlighetsteori. Dette bryter sammen dersom ikke levetidene er identisk fordelte.
For å lage en korrekt hasardrate, h(t), kreves det at levetidene oppfyller kravene til å være grunnlag for MTTF beregning.